法線ベクトルとスムージング角

OpenGLであれ、なんであれ、
3Dグラフィクスプログラミングで一番ネックになりがちなのが、
ベクトルとか行列とか、数学が絡んでくる部分。

ここでは、
法線ベクトルとスムージング角について書いておこうかと思います。
特に、どうやって法線ベクトルを計算するのか、とか、そのあたり。
OpenGLでライティングを使用する場合には、自分で法線を指定する必要があるので、
法線ベクトルの計算は、避けては通れない部分です。

必要な知識は、
・3次元のベクトルの「内積」、「外積」
・OpenGLは、「右手座標系」
・「右手座標系」での回転の向きは「反時計回りが正方向」
とか。
ある程度3次元のベクトルの計算ができる必要があります。
「ベクトルの外積」ってなにさ？とかいう場合は、正直言ってキビシイです。

（以下、数学的にはかなりアバウトなので、そのへんに対してのつっこみは無しということで・・・。）

法線ベクトルとは？

法線ベクトルというのは、
「向きを表す単位ベクトル」です。

単位ベクトルというのは、
長さが1（＝「規格化」されている、とも言う）のベクトルのことです。
また、何の向きを表すのかという意味で、
ここでいう「法線ベクトル」には、2つの種類があります。
・面法線ベクトル
・頂点法線ベクトル
です。

・「面法線ベクトル」
面の向きを表す法線ベクトルです。
面には表と裏があって、
その面の表がどっちを向いているのかを表すベクトルです。

・「頂点法線ベクトル」
面の頂点がどちらを向いているのかを表すベクトルです。
「点に向きなんてあるのか？」といいたいところですが、
「頂点」というよりは、「面の角」といった方がいいかもしれません。
「サイコロの角がどっちを向いているか？」、と聞かれれば、
「サイコロの中心からその角に向かって外側に向いている」、というのは容易に想像できると思います。
その「角がどっちを向いているか？」というのが、頂点法線ベクトルです。


面法線ベクトルの計算

さて、
面法線ベクトルというのは、
「面の向きを表す単位ベクトル」
なわけですが、
もうちょっとひらたい言い方をすると、
「面に垂直で、面の表方向を向いた、長さが1のベクトル」
です。

つまり、面法線ベクトルを決めるには、
・面の表はどっち？
・面に垂直なベクトルを求めるには？
・ベクトルの長さを1にするには？
ということを知る必要があるわけです。

ここでは、具体例として、
ある３角形の面１つについて、
順を追って、その法線ベクトルを求めてみることにします。

で、まずはじめに、その「ある３角形」の各頂点が、次のように定義してあるとしておきます。
（x0、y0、z0とかは、それぞれ頂点座標のx、y、z成分で、適当な値が入っているとします。） 

float[][] v = new float[3][];
//頂点0の座標
v[0] = new float[]{ x0, y0, z0 };
//頂点1の座標
v[1] = new float[]{ x1, y1, z1 };
//頂点2の座標
v[2] = new float[]{ x2, y2, z2 };


・「面の表はどっち？」

OpenGLでポリゴンを表示する場合、たとえば、 

glBegin( GL_TRIANGLES );
glVertex3fv( v[0] );
glVertex3fv( v[1] );
glVertex3fv( v[2] );
glEnd();

と、ポリゴンの周囲に沿って各頂点座標を順に指定していくわけですが、
この頂点の順序で、面の向きが決められます。
面を見たときに、頂点の順序が反時計回りになるのが、表、
時計回りになるのが、裏、です。
回転を表すベクトルで言えば、
回転の向き＝面の向きになります。



・「面に垂直なベクトルを求めるには？」
これを求めるには、
「ベクトルの外積」を使います。

外積って、多少ややこしい感じもしますが、
３次元のベクトルを扱う場合には、結構便利なものなのです。
特に、「垂直」とか「回転」を扱う場合。

で、
どう外積を計算するかというと、
ちょっと数学っぽい形で書くと
(面に垂直なベクトル) = ( v[1] - v[0] )×( v[2] - v[0] )
という感じです。
ベクトルを図に書くと、下のような感じ。

メタセコの画面をちょっと拝借。

ベクトル ( v[1] - v[0] ) と ( v[2] - v[0] ) の外積をとると、
面に垂直で表方向を向いたベクトルが得られます。

まぁ、実際はソースコードに「v[1]-v[1]」なんて書けないので、 どう計算するのかというと、↓ 
/// <summary>
/// ベクトルの外積を求める。
/// <summary>
/// <param name="vector1"> ベクトル1 <param>
/// <param name="vector2"> ベクトル2 <param>
/// <returns>ベクトル1とベクトル2の外積 returns>
public static float[] Cross( float[] vector1, float[] vector2 )
{
    return new float[]{
                          vector1[1] * vector2[2] - vector1[2] * vector2[1],
                          vector1[2] * vector2[0] - vector1[0] * vector2[2],
                          vector1[0] * vector2[1] - vector1[1] * vector2[0]
                      };
}
・・・ソースコード、ベタ張りな感じですが。
このメソッドを使用して、
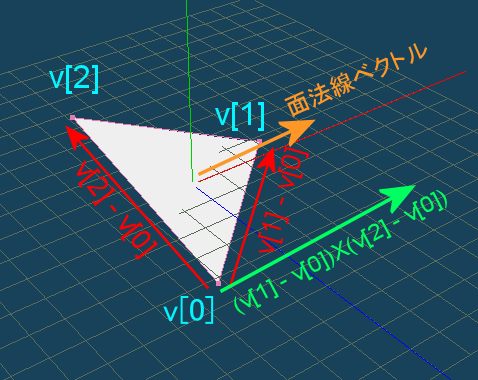
//面に垂直なベクトル
float[] faceVertical = Cross(
                                new float[]{ v[1][0] - v[0][0], v[1][1] - v[0][1], v[1][2] - v[0][2] }, //「v[1] - v[0]」
                                     new float[]{ v[2][0] - v[0][0], v[2][1] - v[0][1], v[2][2] - v[0][2] }  //「v[2] - v[0]」
                                 );
こんな具合です。


・「ベクトルの長さを1にするには？」
 あとは、
先ほど求めた、面に垂直なベクトル「faceVertical 」を
長さを1に（規格化）してしまえば、面法線ベクトルのできあがり。
//ベクトル faceVertical の長さ
float length = System.Math.Sqrt( faceVertical[0] * faceVertical[0]
                                 + faceVertical[1] * faceVertical[1]
                                 + faceVertical[2] * faceVertical[2] );

//面法線ベクトル
//faceVerticalの各成分を長さで割って規格化する。
float[] faceNormal = new float[]{ faceVertical[0] / length, faceVertical[1] / length, faceVertical[2] / length };


これで、三角形のポリゴンの面法線ベクトルは求められるわけですが、
四角形の場合はどうするのか？

いくつか方法があると思いますが、
四角形を三角形２つに分割して、
その三角形２つの面法線ベクトルを平均化する、
というのが一番無難な方法ではないでしょうか。

あ、法線ベクトルの平均化は、
足して２で割ったりしたら、ダメですよ。
長さが1になりませんから。
足した後は、規格化します。

頂点法線ベクトルを求める

基本は面法線ベクトル。
面法線を元に頂点法線を求めます。
ある頂点の頂点法線を求める場合に、
おおざっぱに言ってどのように計算していくかというと、

  1. 頂点法線を求める頂点を共有している面をリストアップする。
  2. リストアップした面の面法線を足しあわせて規格化（＝平均化）したものが、頂点法線。

という具合です。
各面の面法線が求められていて、頂点を共有する面のリストアップさえできてしまえば、
後は、各面の面法線を足しあわせて規格化するだけなので、
たいして難しいことはないです。

スムージング角

で、頂点法線まで求められたとして、
こうして求められた頂点法線をそのまま使って良いのかというと、
実は、そうでもないのです。

たとえば、サイコロの角の頂点。
この頂点の法線の向きは容易に想像できますが、
それを用いて実際に描画すると、ソースコードと描画結果は次のようになります。

glBegin( GL_QADS )

////////////////
// 面1の描画。
// 頂点ごとに頂点法線を指定する。

glNormal3fv( normanl1 ); // 頂点法線を指定。
glVertex3fv( vertex1 );  // 頂点を指定。

glNormal3fv( normanl2 );
glVertex3fv( vertex2 );

glNormal3fv( normanl3 );
glVertex3fv( vertex3 );

glNormal3fv( normanl4 );
glVertex3fv( vertex4 );

////////////////
// 面2の描画。

glNormal3fv ...
...
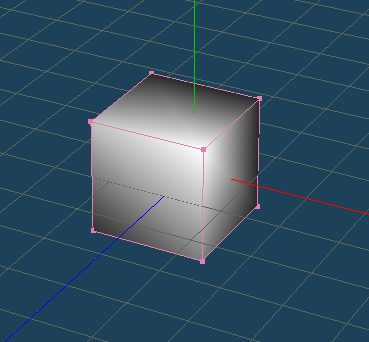
じつは、スムージング角をやたら大きく設定しただけだったりしますが、まぁ、同じことです。

角や辺がはっきりせず、ぼやけてしまいます。
ワイヤーフレームの表示が無かったら、どんな形かすらわからないかも。

一方、頂点法線を使わずに、
面ごとに面法線を指定すると、次のようになります。 

glBegin( GL_QUADS );

////////////////
// 面1の描画。
// 面ごとに面法線を指定する。

glNormal3fv( faceNormal1 ); // 面法線を指定。

glVertex3fv( vertex1 );     // 頂点を指定。
glVertex3fv( vertex2 );
glVertex3fv( vertex3 );
glVertex3fv( vertex4 );

////////////////
// 面2の描画。

glNormal3fv ...
...

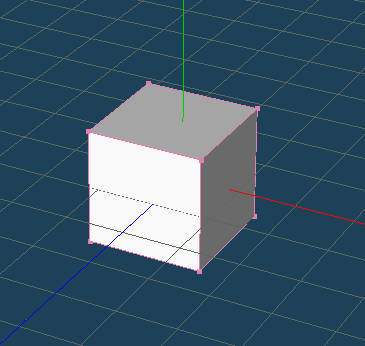
どう見たって、こっちのほうがもっともらしく見えます。
つまり、このようにエッジがある程度鋭いものを描く場合は、
面法線を使うべきなのです。

つまり、エッジがある程度鋭いかどうかをチェックして、
頂点法線と面法線使い分ける必要があるのです。
では、どうやって頂点法線と面法線のどちらを使うかを決めるのか？
ここで、「スムージング角」という角度を導入します。

ある面のある頂点について、
頂点法線と面法線のなす角度が、
このスムージング角より大きければ、面法線、
小さければ、頂点法線を、
その頂点の頂点法線とします。

頂点法線と面法線のなす角度を求めるためには、
ベクトルの内積を利用します。

頂点法線・面法線が、次のように定義されていたとして、 

// 頂点法線
float[] vNormal = new float[]{ x1, y1, z1 };
// 面法線
float[] fNormal = new float[]{ x2, y2, z2 };

この2つのベクトル vNormal, fNormal の内積は、2つのベクトルがなす角をdとして、
vNormal ・ fNormal  = | vNormal | * | fNormal | * cos( d )  =  x1 * x2 + y1 * y2 + z1 * z2
また、法線ベクトルの長さは 1 なので、つまり、
cos( d ) = x1 * x2 + y1 * y2 + z1 * z2
ということは、
d = arccos( x1 * x2 + y1 * y2 + z1 * z2 )
なのです。

こうして求めた角度 d と、あらかじめ決めておいたスムージング角を比較して、
d がスムージング角より大きい場合、
つまり、
面法線と頂点法線の向きが大きく異なる　＝　角が鋭い
場合は、頂点法線を無視して面法線を用います。
d がスムージング角より大きい場合は、
面法線と頂点法線の向きが似ている　＝　角が丸い
ので、そのまま頂点法線を用います。

ただし、描画するたびにこの計算をやるのでは処理が重くなってしまうので、
事前に、
頂点法線をすべて求める → 頂点法線と面法線のなす角を調べ、 → スムージング角より大きければ、頂点法線の値を面法線に置き換える
としておいてから、
頂点法線のみを用いて描画するのが、無難だと思います。

また、 頂点法線と面法線のなす角を調べる場合に、
直接角度を計算するのではなく、
先に cos( スムージング角 ) を求めておいて、これと
頂点法線と面法線の内積( = cos( 頂点法線と面法線のなす角 ) ) を比較すれば、
arccos( ... )を計算する手間が省けます。


<back to OpenGL menu>